Mathematisches und geometrisches Grundwissen
Hier haben wir einige Grundlagen der Mathematik und Geometrie für Sie zusammengestellt, da wenn nicht häufig angewendet, viele einfache Berechnungen vergessen werden. Somit können Sie die Mengen für Ihre Ausschreibung leicht und schnell ermitteln, Planungsunterlagen richtig lesen, sowie die Rechnungen der Unternehmen mit Hilfe der Kostenkontrolle effizient prüfen.
Maßeinheiten
Die wichtigsten Einheiten welche auch auf unseren Seiten vorkommen sind:
| Längeneinheit: | Millimeter (mm), Zentimeter (cm), Meter (m) | |
| 1m | = 1.000mm | |
| 1m | = 100cm | |
| 1cm | = 10mm | |
| 1dm | = 10cm (kein übliches Maß im Bauwesen) | |
| Flächenmaß: | Quadratmeter (m2), Quadratzentimeter (cm2), Hektar (ha) | |
| 1 m2 | = 10.000cm2 | |
| 1ha | = 10.000m2 | |
| Volumen: | Kubikmeter (m3) | |
| Gewicht: | Kilogramm (kg) | |
| Zeit: | Stunden (h), Tage (d), Wochen (woch) | |
| Anzahl: | Stück (Stk.), pauschal (psch) | |
| Winkelmaß: | Grad (°) | |
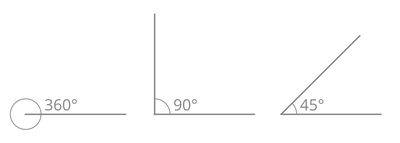 |
||
| Neigung: | wird in Prozent (%) angegeben 100% = 45° / Ausführliche Erklärung Winkel / Neigung. | |
 |
||
Flächenberechnung
Die allgemeine Formel für eine Flächenberechnung lautet: Grundlinie multipliziert mit der drauf senkrechten Höhe. Es folgen einige Beispiele:
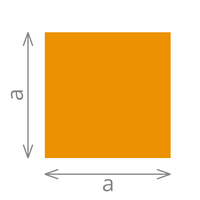
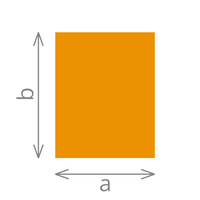
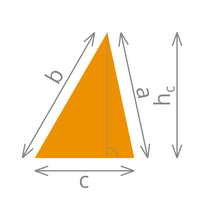
| Das Quadrat | Das Rechteck | Das Dreieck | ||
 |
 |
 |
||
| Fläche= a x a | Fläche= a x b | Fläche= (c x h)/2 | ||
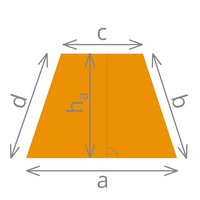
| Das Trapez |
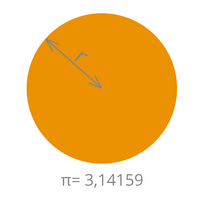
Der Kreis | |||
 |
 |
|||
| Fläche= ((a + c) / 2) x h | Fläche= r² x π |
Berechnung Umfang
Die allgemeine Formel für die Berechnung des Umfanges lautet: Summe aller Seitenlängen. Es folgen einige Beispiele:
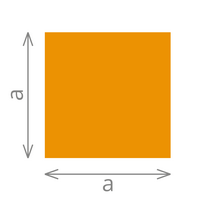
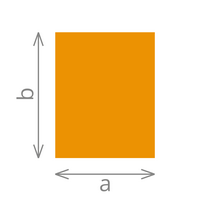
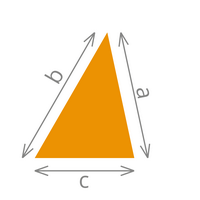
| Das Quadrat | Das Rechteck | Das Dreieck | ||
 |
 |
 |
||
| Umfang= 4 x a | Umfang= (a + b) x 2 | Umfang= a + b + c | ||
| Das Trapez |
Der Kreis | |||
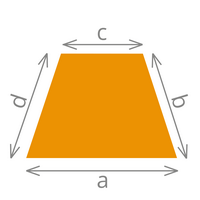 |
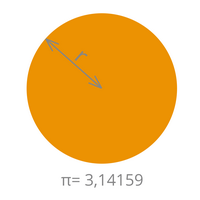 |
|||
| Umfang= a + b + c + d | Umfang= 2 x r x π |
Volumenberechnung
Die allgemeine Formel für eine Volumen-Berechnung lautet: Grundfläche multipliziert mit der drauf senkrechten Höhe.
Die Volumen-Berechnung ist z.B. für die Berechnung der Kubaturwerte notwendig. Es folgen einige Beispiele:
| Der Würfel | Der Quader | |
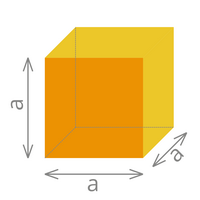 |
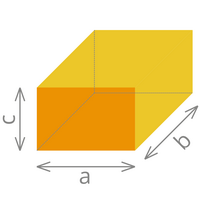 |
|
| Volumen= a x a x a | Volumen= a x b x c | |
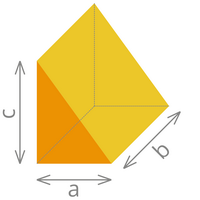
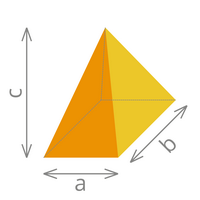
| Der schräge Quader | Die Pyramiden | |
 |
 |
|
| Volumen= (a x b x c)/2 | Volumen= (a x b x c)/3 |
Kubaturberechnung
Im Bauwesen wird die Gesamtkubatur unterschieden in: unterirdische, oberirdische und urbanistische Kubatur.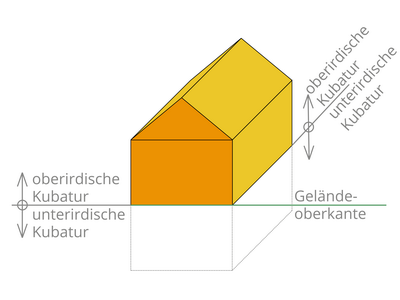
Gesamtkubatur (leer für voll)
Diese ist definiert durch die gesamten Abmessungen des Bauwerks, d.h. das komplette Bauwerksvolumen, inkl. eventueller unterirdischer Räume, sowie Dachgeschoss usw. (Summe der unterirdischen und oberirdischen Kubatur)
Unterirdische Kubatur
Die unterirdische Kubatur definiert sich durch die Volumensabmessungen unterhalb der (geplanten) Geländeoberkante.
Oberirdische Kubatur
Diese Kubatur definiert sich durch die Volumsabmessungen oberhalb der (geplanten) Geländeoberkante.
Urbanistische Kubatur
Als urbanistische Kubatur wird das Gebäudevolumen oberhalb der Geländeoberfläche bezeichnet, das aufgrund der Außenmaße berechnet wird. Nicht berechnet werden Dachräume mit einer Höhe von nicht mehr als 2,00m, senkrecht gemessen von der Oberkante der Dachhaut; sowie technische Volumina die erforderlich sind, um bestehende Gebäude an die Bestimmungen des Brandschutzes, der Beseitigung architektonischer Barrieren und der Wärmedämmung anzupassen.
(Auszug aus den Durchführungsbestimmungen der Südtiroler Gemeinden)
Die Urbanistische Kubatur muss abhängig von der betroffenen Gemeinde laut geltenden Durchführungsbestimmungen berechnet werden. Diese können von Gemeinde zu Gemeinde unterschiedlich sein. z.B. wird nicht immer der Dachboden als urbanistische Kubatur angerechnet bzw. nicht berücksichtigt.
Grundlagen Massenberechnung
Einheit ist nicht gleich Einheit
Es kann häufig vorkommen dass auf den Planunterllagen verschiedene Einheiten angegeben werden (z.B.: mm, cm, m). Bevor Sie nun Flächen oder Volumen berechnen, müssen Sie die verschiedenen Einheiten auf eine gemeinsame Einheit bringen, d.h. es dürfen NIEMALS mm, cm und m miteinander addiert, subtrahiert, multipiziert oder dividiert werden. Dies würde zu einem falschen Ergebnis führen.
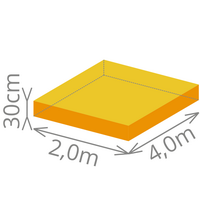
| Falsch! | 2,00m x 4,00m x 30cm / 2 x 4 x 30= 240 ? |
| Richtig | Zuerst Einheiten Vereinheitlichen: 30cm = 0,30m => 2,00m x 4,00m x 0,30m = 2,4m³ |
Prozente %
Das Prozentzeichen (%) werden Sie öfters antreffen, dies kann eine Neigung angeben, es findet aber auch Anwendung bei Argumenten wie Rabatte, Mehrwertsteuer, Aufpreise, Kostenaufteilung u.a.m. Prozent kommt aus dem Latein und bedeutet von Hundert.
6% => 6 von Hundert => 0,06
Beispiele:
| A) | 6% Rabatt / Skonto werden vom Ganzen abgezogen: 1,0 – 0,06 = 0,94 14.400€ wird um 6% Skonto reduziert: 14.400€ x 0,94 = 13.536€ oder 14.400€ x 6 / 100 = 864€ werden vom Grundpreis abgezogen = 13.536€ |
| B) | 5% + 2% Rabatt / Skonto Sie erhalten bei der ersten Verhandlung 5% Rabatt und beim zweiten Anlauf erziehlen Sie weitere 2%. Das Unternehmen bestätigt Ihnen 5%+2% Achtung: das sind nicht 7% Erklärung: 10.000€ – 5% = 10.000€ x 0,95 = 9.500€ – 2% = 9.500€ x 0,98 = 9.310€ 10.000€ – 7% = 10.000€ x 0,93 = 9.300€ Der Unterschied ist erträglich, jedoch gibt es einen. |
| C) | 10% Mehrwertsteuer (IVA) Wird dem Ganzen hinzugefügt: 1,0 + 0,10 = 1,10 7.500€ + 10% MwSt. = 7.500€ x 1,10 = 8.250€ |
| D) | 18% Aufpreis Wird dem Ganzen hinzugefügt: 1,0 + 0,18 = 1,18 Das Fenster mit Dreifach-Verglasung kostet z.B. 18% mehr, als das Ihnen angebotene Fenster mit Zweifach-Verglasung: 760€ + 18% Aufpreis: 760€ x 1,18 = 896,8€ |
| E) | 25% Anzahlung Dies drückt einen Anteil vom Ganzen aus: 0,25 Bei fortschreitender Arbeitsausführung, stellt Ihnen das Unternehmen eine Anzahlung in Höhe von 25% vom Gesamtauftrag, welcher z.B. bei 76.000€ liegt: 76.000€ x 0,25 = 19.000€ |
Flächenaufteilung
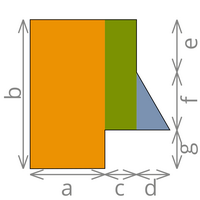
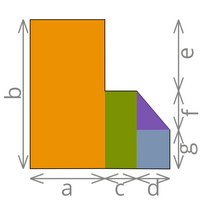
Sollten Sie eine unregelmässige Fläche vorfinden (Grundrisse, Fassaden, usw.), haben Sie die Möglichkeit die Gesamtfläche in beliebig viele kleinere, geometrisch definierte Flächen zu unterteilen, die Summe der kleinen Flächen ergibt die Gesamtfläche.
| Beispiel 1 | Beispiel 1 |
|
|
|
| Fläche = Rechteck + Rechteck + Dreieck | Fläche = Rechteck + Rechteck + Rechteck + Dreieck |
| Fläche = (a x b) + [c x (f +e)] + (d x f /2) | Fläche = (a x b) + [c x (g +f)] + (d x g) + (d x f /2) |
„Doppelte Ecken“
Bei Volumensberechnungen für die Mengenangaben möchten wir Sie auf eine möglichen Fehler hinweisen:
In der Regel werden auf den Planunterlagen die Aussenmaße eines Grundrisses angegeben (Abb. 1).
Werden nun diese Maße zu einer Gesamtlänge der Wände aufsummiert und anschliessend mit der Wandstärke und Wandhöhe multipliziert, so werden die Ecken stets doppelt berechnet.
RICHTIGE MESSMETHODEN:
- Abb. 2: Summieren Sie die Mittellinie der Wände und multiplizieren Sie diese mit der Bauteilstärke und -höhe.
oder
- Abb. 3: Teilen Sie die Bauteile immaginär, laut Abbildung, in mehrere Bauteile und summieren Sie die Längen aller Bauteile. Anschliessend multiplizieren Sie diese wiederum mit der Bauteilstärke und –höhe.
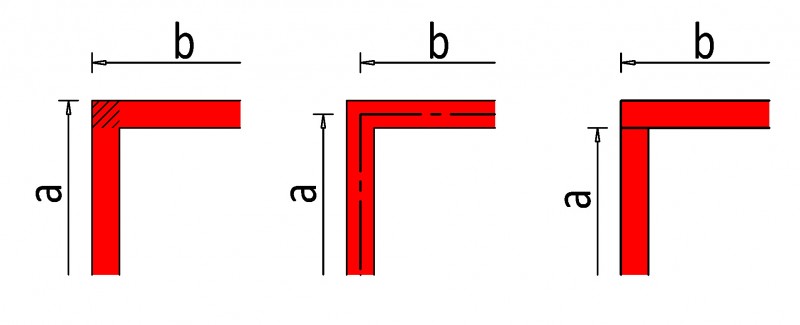
Abb. 1 Abb. 2 Abb. 3
Winkel / Neigung
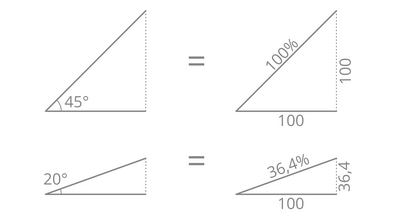
Der Unterschied zwischen den beiden Einheitsgrößen besteht darin, dass der Winkel die „Öffnung“ zwischen zwei Linien beschreibt und in Grad [°] angebenden wird, während die Neigung, das Gefälle bzw. die Steigung einer Linie bezogen auf die Horizontale angibt und in Prozent [%] angegeben wird. 100% entspricht 45°

Winkel [°] Neigung [%]
Achtung: 100% wird fälschlicherweise oft als senkrecht verstanden
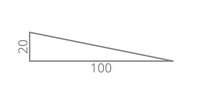
Prozent % kommt aus dem Latein und bedeutet “von Hundert” => 20% bedeutet 20 von 100 und ergibt einen Winkel von 11,5°
Die Einheit darf dabei vernachlässigt werden, sofern es bei beiden Strecken dieselbe Einheit sind: 20cm pro 100cm entspricht genauso viel wie 20m pro 100m, 20mm auf 100mm usw.; die Neigung bleibt unabhängig von der Einheit identisch.
20% auf einer Länge von 200 würde 40 ergeben, hier die grafische Erklärung dazu:
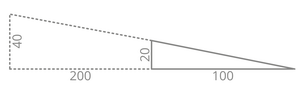
Die Prozentangabe ist für die Baustelle geeigneter als die Angabe von Winkel. Mit einem normalen Maßband und einer Wasserwage lassen sich Prozente leicht auftragen bzw. messen.
Bruttowohnfläche / Nettowohnfläche
Die Bruttowohnfläche (Abb. 1) umfasst sämtliche Flächen innerhalb der Gebäudehülle, inklusive aller Wandquerschnitte und wohnungsinterner Treppen. Außenliegende Flächen wie Treppenhäuser, Terrassen, Balkone sowie nicht bewohnbare Keller- und Dachgeschossräume werden nicht berücksichtigt.
Die Nettowohnfläche (Abb. 2) bezeichnet die Summe aller begeh-, beleg- und bewohnbaren Bodenflächen einer Wohnung, inklusive wohnungsinterner Treppen. Ausgeschlossen sind: Wandquerschnitte aller Außen- und Innenwände, Tür- und Fensternischen, sowie aller Außenbereiche und Raumabschnitte die niedriger als 1,5m sind.
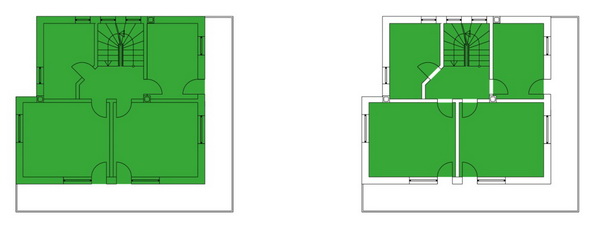
Abb. 1: Bruttowohnfläche Abb. 2: Nettowohnfläche
Richtlinien zu den Abzügen in Wandflächen
Abzüge bei Öffnungen (Fenster und Türen)
Sind in einem Bauteil Öffnungen vorhanden, so werden diese ab einer bestimmten Abmessung, teilweise von der gesamten Menge der Wandfläche abgezogen. Die Realisierung der Öffnung und der dazugehörigen Laibung muss dem ausführenden Unternehmen vergütet werden, daher wird nicht die gesamte Öffnung zum Abzug gebracht.
| Abzüge | |
| Erdarbeiten | ab 1m³ bzw. 1m² |
| Betonarbeiten (Nischen Kassetten Hohlkörper) | ab 0,5m³ bzw. ab 2,5m² |
| Betonarbeiten (Schlitze) | ab 0,1m³/m |
| Betonerhaltungsarbeiten (Abb. 3) | ab 2,5m² |
| Metallbauarbeiten | ab 0,5m³ bzw. 2,5m² |
| Mauerwerksbauteile | ab 2,5m² bzw. 1m |
| Trennwände | ab 2,5 m² |
| Estricharbeiten | ab 0,1m² |
| Bodenbeläge (Fliesen, Parkett, Pflasterungen, usw.) | ab 0,1m² bzw. 1,0m |
| Putz- und Stuckarbeiten | ab 2,5m² |
| Trockenbauarbeiten (Abb. 2) | ab 1,0m² |
| Wärmedämm- Verbundsysteme | ab 1,0m² |
| Naturwerksteinarbeiten | ab 0,5m³; bzw. 0,1m²; bzw. 1,0m |
| Malerarbeiten | ab 2,5m² |
| Fassadenarbeiten | ab 2,5m² |
| Tischlerarbeiten | ab 2,5m² bzw. 1,0m |
| Zimmerer- und Holzbauarbeiten (Wänden und Decken) | ab 2,5 m² bzw. ab 1,0m |
| Zimmerer- und Holzbauarbeiten (Böden) | ab 0,5 m² bzw. ab 1,0m |
| Dachdeckungs- und Dachabdichtungsarbeiten | ab 2,5m² bzw. 1,0m |
Öffnungen, welche kleiner sind als die oben angegebenen Werte, werden nicht abgezogen, siehe Abb. 1.
Bei Öffnungen, welche größer sind als die oben angegebenen Werte, wird das überschüssige Maß abgezogen, siehe Abb. 2 und Abb. 3.
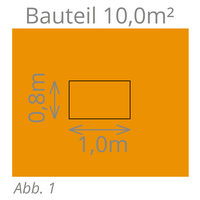
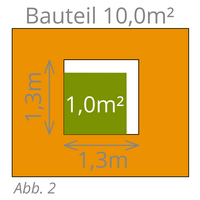
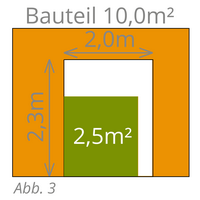
| Beispiel Abb. 1: z.B. Trockenbauarbeiten ab 1,0m² | |||
| Bauteil: | 10,0 m² | (Beispiel Bauteilabmessung) | |
| Öffnung: | 1,0 x 0,8 m = | 0,80 m² | (Abzug ab 1,0m², daher kein Abzug) |
| Menge Massenberechnung: | 10,0 m² | ||
| Beispiel Abb. 2: z.B. Trockenbauarbeiten ab 1,0m² | |||
| Bauteil: | 10,0 m² | (Beispiel Bauteilabmessung) | |
| Öffnung: | 1,3 x 1,3 m = | 1,69 m² | (Abzug ab 1,0m²) |
| Differenz über 1,0 m² | -0,69 m² | ||
| Menge Massenberechnung: | 9,31 m² | ||
| Beispiel Abb. 3: z.B. Malerarbeiten ab 2,5m² | |||
| Bauteil: | 10,0 m² | (Beispiel Bauteilabmessung) | |
| Öffnung: | 2,0 x 2,3 m = | 4,60 m² | (Abzug ab 2,5m²) |
| Differenz über 2,5 m² | -2,10 m² | ||
| Menge Massenberechnung: | 7,90 m² | ||